ANOVA con el software estadístico MINITAB
Índice del Artículo
ANOVA CON UN SOLO FACTOR
Hipótesis nula: No existen diferencias en media en cuanto a los niveles del factor respecto a la variable de respuesta continua Y.
Hipótesis alternativa: Existen diferencias en al menos un par de medias.
Supuestos de partida de Normalidad de los residuos y Homocedasticidad
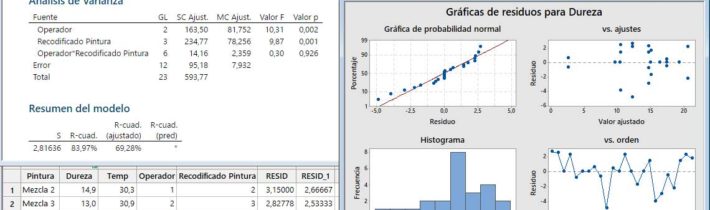
Tabla ANOVA
La Tabla ANOVA resulta significativa, el p-valor asociado al estadístico F es menor que 0,05, luego existen diferencias en media poblacional en la variable dependiente de respuesta de la medición de dureza, respecto de algún operador a otro.
Se compara si las medias de la variable respuesta son las mismas en los 3 o más grupos que define la variable independiente o factor. Si el Test en la Tabla ANOVA resulta estadísticamente significativo, se comprueba con unas pruebas POST HOC como las de Tukey, entre que par de medias se presentan esas diferencias significativas, esto es, en aquellas comparaciones múltiples donde el 0 no está dentro del intervalo de confianza, es decir, donde la línea vertical discontinua de rayitas, no toca el gráfico subyacente:
ANOVA CON 2 FACTORES Y LA INTERACCIÓN
1º Hipótesis nulas de EFECTOS PRINCIPALES: No existen diferencias en media en cuanto a los niveles de cada factor principal respecto a la variable de respuesta continua Y (efectos principales de cada uno de los factores).
2º Hipótesis de la INTERACCIÓN.
Supuestos de partida del ANOVA BIFACTORIAL
Respecto a la comprobación de los supuestos del modelo, con los Gráficos 4 en 1 del botón ‘Gráficas‘ del submenú del modelo lineal general del ANOVA. Previamente a la interpretación de resultados de la Tabla ANOVA, es necesario validar los supuestos de partida del Análisis Estadístico, esto es Normalidad y Homocedasticidad de los residuos (varianza constante, que se puede apreciar en la segunda gráfica en horizontal de valor ajustado, si los datos tienen forma de altavoz-megáfono se puede intuir un problema respecto a este supuesto, que habrá que comprobar analíticamente con la prueba de esfericidad de Bartlett), así como independencia y aleatoriedad de los errores, cuyo cumplimiento queda fuera de lugar ante una situación como la del 4º gráfico, lo más lejano a una gráfica de zig-zag de aleatoriedad en los residuos.
La Tabla ANOVA o ADEVA sirve en estadística para testear si la media poblacional de la variable de respuesta de 3 o más grupos, es la misma respecto a cada 1 de los 2 Factores, en lo que se denomina efectos principales. Se estudia, de manera complementaria si la interacción de los Factores, influye en la medición de la variable dependiente, es decir, si es estadísticamente significativa. Siempre partiendo de que se cumplen los supuestos de partida de Normalidad de los residuos o errores y Homocedasticidad en las varianzas de los mismos o las de la variable dependiente.
Si el Factor no está recodificado a número, se hace mediante la barra de menús de ‘Datos’, con lo que efectivamente ahora es cuando se puede realizar la Tabla ANOVA, una vez redefinidas las categorías de la variable explicativa.
Al contrario que ocurre en SPSS, en Anova de 2 Factores con el paquete Minitab, hay que especificar la interacción, y agregarla al análisis estadístico, para su posterior evaluación de significación estadística en la Tabla ANOVA, un p-value menor que 0,05 implica que la interacción de ambos factores influye en nuestro análisis.
En la Tabla Anova de la captura de pantalla del visor de la sesión de trabajo, valores p menores que 0,05 nos exponen diferencias estadísticamente significativas, ya sean en los factores por separado (efectos principales), como en la interacción de ambos. El coeficiente de determinación ajustado nos habla acerca de la bondad del modelo y de la proporción de variabilidad explicada por la regresión.
El p-valor asociado al estadístico de Anderson-Darling de normalidad es mayor que 0,05, luego se cumple el supuesto de distribución normal de los errores.
El p-valor asociado a la prueba de esfericidad de Bartlett de homogeneidad de varianzas es mayor que 0,05, por lo que concluye con que se cumple el supuesto de homocedasticidad de los residuos.
Pruebas POST HOC de comparaciones múltiples
Puebas Post Hoc de Tukey para comparaciones múltiples de medias, se trata de detectar qué combinaciones de tratamientos (igualdad de medias 2 a 2),de los factores o variables explicativas, y de incluso la interacción, presentan diferencias estadísticamente significativas.
Los cruces de pares de medias que no comparten una letra en la combinación de las categorías de cada factor, son significativamente diferentes desde un punto de vista estadístico.
estamatica@gmail.com