Tutorial de JAMOVI, software estadístico gratuito
Breve tutorial del paquete estadístico de software libre JAMOVI, una opción recurrente a otros software de pago a nivel de empresa, como pueden ser SPSS o MINITAB, y con el que se pueden llevar a cabo la mayor parte de análisis estadísticos que tienen lugar en Tesis, TFM, TFG y Abstract y publicaciones científicas. JAMOVI facilita el uso del lenguaje de programación R a través de su interfaz gráfica, en continua actualización.
Índice del Artículo
ABRIR ARCHIVOS DE EXCEL, SPSS o STATA
Se pueden abrir archivos de bases de datos en Excel (.xlsx), Spss (.sav), o Stata en JAMOVI, en cambio la opción de importar nos genera 3 variables (columnas) que posteriormente tenemos que eliminar.
DEFINIR VARIABLES
Se pueden definir y modificar los tipos de variables en Jamovi, con tan solo hacer clic en la propia variable en la tabla de nuestra base de datos de trabajo.
GENERAR VARIABLES A PARTIR DE OTRAS
Ejemplo: Crear una variable suma de las puntuaciones de los ítems, a través de la suma de los valores de los ítems de una dimensión subyacente.
RECODIFICAR VARIABLES
TRANSFORMAR VARIABLE LIKERT CATEGÓRICA EN NUMÉRICA ORDINAL
GRÁFICOS
SCATTERPLOT (AÑADIR MÓDULO JAMOVI)
Gráfico de dispersión scomo módulo a añadir en JAMOVI.
TABLAS DE FRECUENCIAS
Tablas de frecuencias para variables categóricas o marcas de clase de variables continuas tipo intervalo, con opciones de estadísticos descriptivos de tendencia central y de dispersión o variabilidad.
MATRIZ DE CORRELACIONES
Existe la posibilidad de ver como interactúan 2 o más variables a través de la regresión, el análisis de correlaciones y el cruce de categórica a través de la chi-cuadrado.
CHI-CUADRADO
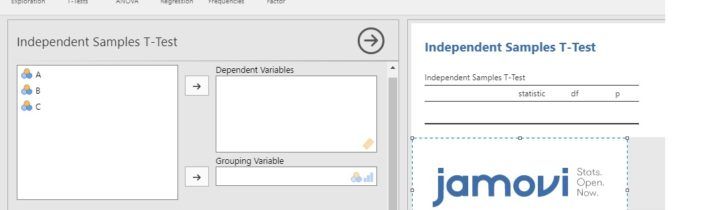
T DE STUDENT MUESTRAS INDEPENDIENTES
JAMOVI ofrece la posibilidad de obtener el tamaño del efecto a partir de la d de Cohen (Cohen’s d), y de esta manera contrastar no solo si las diferencias en media son estadísticamente significativas, sino además si son clínicamente relevantes (d>0,8). Además ofrece la posibilidad de la casilla de verificación del Test de Welch’s, en el caso de no cumplirse la hipótesis de partida de homogeneidad de varianzas, y la U de Mann-Whitney (comparativa de medianas),si se viola gravemente la normalidad, y el tamaño muestral es pequeño.
T DE STUDENT MUESTRAS RELACIONADAS
Se procede a realizar la T de Student de muestras relacionadas en JAMOVI cuando a los mismos individuos se les pasa por 2 tratamientos, o tenemos una medición de un antes y una medición de un después.
ANOVA DE UN FACTOR
El objetivo de la Tabla ANOVA (Analysis of Variance) es poner a prueba si existe una diferencia estadísticamente significativa entre las medias de más de 2 grupos independientes ,es decir añadir un nuevo grupo a la comparativa de las medias de 2 grupos de la de T de Student.
La hipótesis nula del ANOVA plantea que no hay diferencia entre las medias poblacionales de los grupos. Por el contrario, la hipótesis alternativa plantea que no todas las medias poblacionales son iguales, es decir, que al menos un par de medias difieren.
Las puntuaciones de la variable dependiente (Y) deben distribuirse de manera Normal y Homocedástica en cada grupo. ¿Cómo saber si se cumple este supuesto de partida?. Dentro del procedimiento One-Way ANOVA, hay un apartado para comprobar los supuestos de la prueba (Assumption Checks), en el que se incluye un test de Normalidad (Normality test) por un lado, y por otro lado, el ANOVA se basa en el supuesto de homogeneidad de varianzas. ¿Cómo saber si se cumple este supuesto?. Se puede llevar a cabo una prueba de homogeneidad de varianzas, el test de Levene, que se incluye de manera opcional dentro del procedimiento One-Way ANOVA. Si dicho test resulta estadísticamente significativo, se considera más conveniente el llevar a cabo la prueba de Welch, más conservadora que el propio ANOVA.
Pruebas Post-Hoc de comparaciones múltiples a posteriori
Cuando no se rechaza la hipótesis nula del ANOVA, concluimos que todas las medias de los grupos son iguales entre sí. Sin embargo, si la Tabla ANOVA o la prueba de Welch resultan estadísticamente significativas, implica que al menos dos de los grupos tienen una media diferente. En ese caso, interesa determinar entre qué grupos, en particular, existen diferencias.
La prueba de Tukey es el test a tener en cuenta en caso de homogeneidad de varianzas, la de Games-Howell en el caso de violación de este supuesto del ANOVA. Resultan estadísticamente significativas aquellas diferencias de medias entre cruces de 2 grupos cuyo p-valor sea menor de 0,05, siempre trabajando con una confianza del 95%, fijada para la investigación.
KRUSKAL-WALLIS (EQUIVALENTE NO PARAMÉTRICO AL ANOVA)
En el caso de violación grave de los supuestos de partida de normalidad y homocedasticidad, o si se trata de variables de tipo Likert (ordinal), se procede con el Test de Kruskal-Wallis de comparativa de medianas de los 3 o más grupos, como sustituto del ANOVA paramétrico.
ANOVA DE 2 FACTORES
Una vez se comprueba la significatividad estadística de la Tabla Anova, se llevan a cabo las pruebas Post-Hoc de comparaciones múltiples de medias de las muestras 2 a 2, para detectar entre que pares de medias de los grupos se aprecian diferencias estadísticamente significativas (p-valor<0,05).
ANOVA DE MEDIDAS REPETIDAS
Una vez comprobado el supuesto de normalidad de las 3 muestras, en por ejemplo 3 o más tratamientos sobre los mismos individuos (casos), comparar si se comportan de la misma manera en media, a partir de la variabilidad de cada muestra.
ANCOVA
Comparativa de medias de la variable dependiente de respuesta en los diferentes grupos (muestras), una vez se elimina la influencia de la covariable continua ‘Edad’.
FIABILIDAD Y VALIDEZ BATERÍA DE TEST (PSICOMETRÍA)